. . . you will take [careful] observations of latitude & longitude
Thomas Jefferson was as interested in the methods and equipment for “ascertaining by celestial observation the geography of the country” as with any other single aspect of the Expedition. He played an important role in making sure that Lewis purchased the proper equipment and learned how to use it before he left for the West. He also insisted that observations be conducted with accuracy, would be redundant, would be comprehensible to others, and that sufficient copies of all observations would be made to guarantee against the possible loss of one or more sets. As faithfully as they could, the captains complied with the President’s wishes.
Latitude
For Lewis and Clark, as for so many of their predecessors and contemporaries, calculating latitude was far simpler than calculating longitude. In the northern hemisphere, latitude may be derived by measuring the angle made between the North Star and the horizon. Crude instruments to obtain this angle have existed for thousands of years and by the time of Lewis and Clark, instruments like the sextant and octant, only slightly less precise than those available to us, were in use.
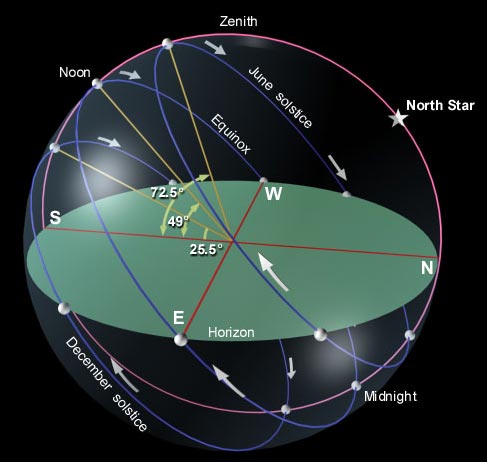
Figure 1 shows graphically what an ephemeris shows in tables. The difference is that the astronomical almanac gives figures for solar (sun), lunar (moon), and astral (star) altitudes for every day of the year along all lines of latitude whereas the diagram indicates only solar altitude at 4 times during the year (equinox and solstice) and only along one line of latitude. What line of latitude? That can be determined from the diagram below as follows: on 21 June, at its zenith or highest point in the sky (local noon) the sun is directly overhead (an altitude of 90°) at latitude 23°30′ N (the Tropic of Cancer). If the altitude of the noon sun at the point of observation on 21 June is 72°30′ (the symbol ‘ indicates a “minute,” and 60 minutes equal one degree), then the latitude of the point of observation is 41°N. This is derived from subtracting 72-1/2 degrees (altitude of the sun at observation point) from 90 degrees (altitude of sun at Tropic of Cancer) and then adding the result (17-1/2 degrees) to the latitude of the Tropic of Cancer (23-1/2 degrees) where the sun’s altitude is 90°. To use the ephemeris, all one needs to know is the day of the year and the altitude of the sun, the moon, or one of the key stars such as Betelgeuse, Aldebaran, Antares, or Vega.
Latitude may also be calculated by measuring the altitude of the sun, moon, or certain planets and stars above the horizon on known days and reading latitude from tables designed for that purpose. It was not much more difficult for the captains to measure these altitudes with a sextant or octant and to calculate latitude using one of the three ephemerides or astronomical almanacs they carried. These contained tables showing the daily position of celestial bodies such as the sun, the moon, and key stars. Calculating latitude gave Lewis and Clark few problems and their readings were accurate to within a fraction of a degree.
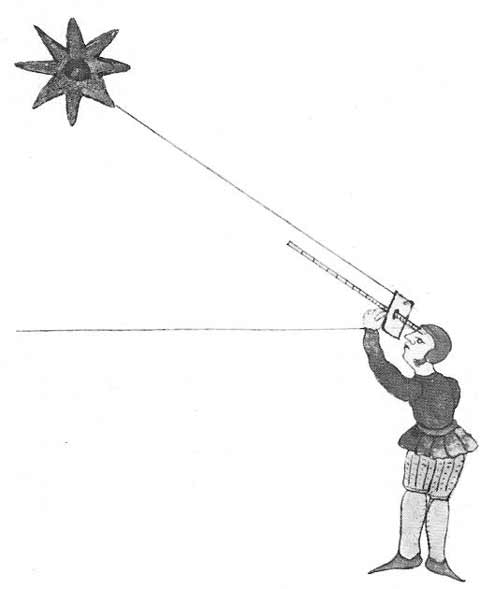
In Figure 2, an illustration from a 16th century portolan atlas, a seaman is determining latitude using a cross-staff. This device allowed him to measure the “altitude” of Polaris or the North Star. Polaris is directly overhead at the North Pole (90° of latitude); in other words, the angle between Polaris and the horizon at the North Pole is 90°. This angle is called “the altitude” of Polaris. At the Equator (0° of latitude), the North Star is on the horizon, making an angle of 0°.
For any point between the Equator and the North Pole, latitude is obtained simply by measuring the altitude of Polaris: at 30°N the star is 30° above the horizon, at 63°N, it is 63° above the horizon, and so on. Before the use of the cross-staff pictured, mariners and others who needed to determine latitude used flat pieces of wood with holes to sight through to locate Polaris and with pieces of cord attached to measure angles.
Longitude
For much of the early era of global exploration, longitude had been difficult to calculate because either an elaborate set of astronomical tables and measurements were required or an accurate time-keeping device was necessary, and neither was available until the 18th century. As early as 1610 Galileo had devised a way to determine longitude by observation of the passage of the 4 moons of Jupiter.
By the early 18th century, while still using the transit of Jupiter’s moons, navigators had learned to make approximate calculations of longitude by observing the changing angular distance between the Moon and a prominent star such as Antares. But numerous careful observations and extensive calculations were required for this method to work and neither of these was really feasible on board ship or in the field.
Finally, in 1735, partially in response to an offer of £20,000 by the British government to anyone who could solve the problem of determining longitude at sea, an English clockmaker named John Harrison devised a working spring-based chronometer that showed promise of a solution. Numerous sea trials and several improved versions of Harrison’s original model were required before, in 1773, Harrison had a working chronometer, durable enough for extensive field observation. It was a version of this chronometer that Lewis and Clark carried with them.
All this seems quite simple. Why, then, were the captain’s longitudinal observations so prone to error? The answer is also simple: they did not have, as we do, reliable battery-powered watches with quartz movements. When their chronometer ran down, it had to be re-calibrated on local time, which required them to make observations to determine the sun’s zenith or local “noon” and then setting the chronometer by estimating the Expedition’s current longitudinal position. Over the course of their journey, the small incremental errors produced by this procedure became larger ones.
There were other methods of calculating longitude available to them, using astronomical observation. But many astronomical readings had to be acquired over the course of a night in order to obtain sufficiently precise data to determine longitude. It was asking a lot for men exhausted by the rigors of their daily trek, to spend three or four hours in the cold and damp of a mountain night taking sightings of the moon and stars, recording observations, and making calculations by firelight. It was only natural that errors would exist in data obtained in this manner. Even the most skilled astronomer or surveyor would have been hard pressed to make highly accurate observations under such circumstances.
Calculating Longitude
Longitude can be calculated using either time or astronomical observation. Calculating longitude by chronometer is based on the fact that any point on the earth’s surface moves through a complete circle of 360 degrees once in a 24-hour period; during 1 hour, any point on the earth’s surface moves through an east-to-west 15° arc of a full circle. If time can be fixed along any meridian of longitude, then longitudinal distance can be determined by comparing time at that meridian with local time, usually based on the point at which the sun reaches its zenith.
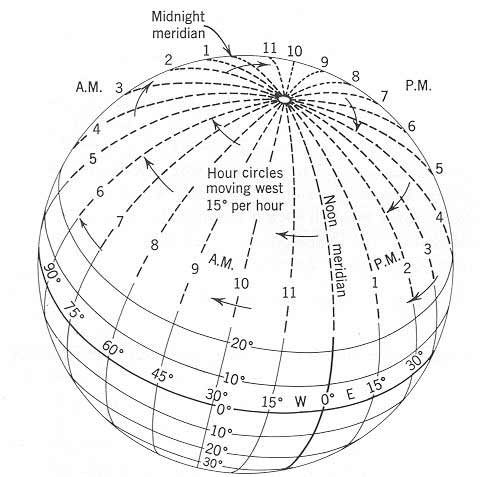
From Figure 3 it can be seen that if it is noon along the prime or Greenwich meridian of longitude, it will be 1:00 pm 15° to the east and 11:00 am 15° to the west. These times are referred to respectively as being “ahead” or “behind” Greenwich Mean Time (GMT), or time along the prime meridian. Using this principle, it is easy to determine longitude. For example, if a chronometer set on Greenwich Mean Time reads 6:00 pm or 1800 GMT at the time when the sun reaches its highest point in the sky (local noon) from the vantage point of the observer, then the sun reached its zenith over the prime meridian 6 hours earlier. The observer is, therefore, 90° west of prime meridian (6 hours x 15° = 90° of longitude). Since local sun time is different everywhere from GMT, trying to keep track of train schedules on east-west routes became impossible by the mid-19th century and so, by international convention in 1877, standard time zones of approximately 15° of longitudinal width were established, centered on 0°, 15°E and W, 30°E and W, and so on. Within each time zone, time is the same everywhere, rather than being kept locally.
Measurement Errors
The errors that Lewis and Clark made in latitude and longitude calculations were less the result of their instruments, their mathematics, or field conditions than by small errors of three types that affect all astronomical observations:
(1) miscalculating refraction or the bending of light in the atmosphere, which causes altitudes to appear slightly greater than they actually are;
(2) estimating semidiameter of either the sun or moon, the discs of which are too large to be used entire when making a sighting. Therefore it is necessary to sight the “sun’s upper limb” or top half or the “moon’s lower limb” or bottom half and then correct by calculation to obtain a reading at the center of the disc; and
(3) correcting for “parallax,” the fact that while navigational tables are based on distances and angles calculated from the earth’s center, observations are made from the earth’s surface.
Recognition
. . . that they may with certainty be recognised hereafter.
After the Expedition Jefferson noted that “it is only to latitudes that [their] map may be considered as tolerably correct, not as to its longitudes.” This was overly critical: certainly the captains’ longitude observations were less than perfect. Yet William Clark‘s ultimate map of the western portion of North America, based in part on those observations, nevertheless proved quite accurate in its longitudinal reckoning. In the final analysis, in spite of the extant errors, their longitudinal observations were better than could or should have been expected. The ultimate results of their “observations of latitude & longitude” bore that out.
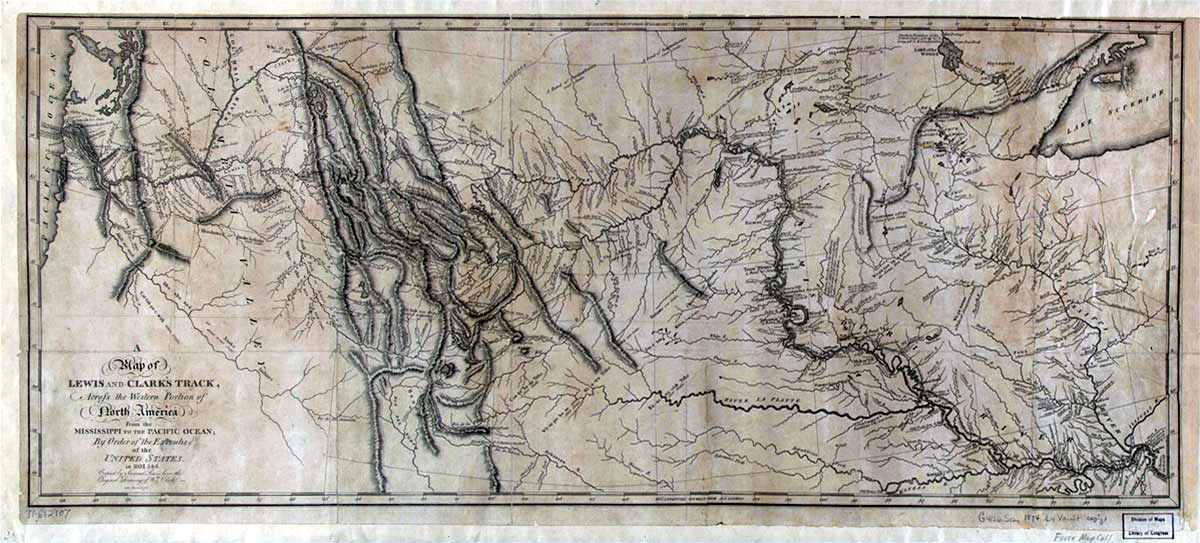
Clark’s final map was the culminating piece of geographical information emerging from the Expedition and resulting directly from Jefferson’s injunction to preserve knowledge for the future. Completed in manuscript form by 1811, engraved and published with the Nicholas Biddle History of the Expedition . . . in 1814, it portrayed with artistry, skill, and accuracy the area through which the Expedition had passed. Course and distance information is apparent on that map and coordinate positions are accurate to within 5%, an accuracy level that would not be matched by many cartographers until the advent of mapping aided by aerial photography in the early 20th century.
Clark’s map represented the ultimate triumph of the vertical perspective, the ability to synthesize mental and actual maps and to portray geographical features with precision in the context of the geographic coordinate system within which he operated.
Clark’s Final Map
William Clark began this map at Fort Clatsop during the winter of 1806. He continued to revise it for several years after his return, drawing upon new information from Zebulon Pike as well as from John Colter and George Drouillard, both veterans of the expedition. The size of the original is 25-5/8 by 11-7/8 inches. Clark presented a more accurate picture of the Rocky Mountains than anyone had previously imagined, as may be seen in a comparison with the pre-expedition map drawn by Nicholas King.
Clark’s map, like the other geographical results of the Expedition, set the standard for other explorers to follow and, although America’s first great territorial mapping project did not achieve all the scientific precision the President had wished for, it was enough. The mental maps had become actual maps and an American claim over territory from the Mississippi to the Pacific was secured.