Editor’s Foreword
Known now as the “Astronomy Notebook,” this extraordinary document has been an obscure and often neglected detail in the history of the Lewis and Clark Expedition. Yet there are few other pre-expeditionary documents that are equal to it in importance, for it contains the keys to the fulfillment of Jefferson’s primary charge to Lewis: “Beginning at the mouth of the Missouri, you will take observations of latitude & longitude, at all remarkable points on the river, & especially at the mouths of rivers, at rapids, at islands, & other places . . . as that they may with certainty be recognised hereafter. . . . The variations of the compass too, in different places, should be noticed.” All those observations were to be taken, he emphasized, “with great pains & accuracy,” and ultimately submitted to the Secretary of War, who would have the calculations completed “by proper persons.”[1]Autograph document signed; sender’s copy (Library of Congress). Reprinted in Donald Jackson, ed., Letters of the Lewis and Clark Expedition with Related Documents, 1783-1854, 2d ed., 2 vols. … Continue reading
Although no author’s name appears on the document, it clearly is the work of Robert Patterson of Philadelphia, Pennsylvania. His authorship is easily traced through reference to a letter that Patterson wrote to Thomas Jefferson on 15 March 1803,[2]Ibid., 1:28-31. in which Patterson detailed his method for computing longitude from an observation for Lunar Distance. The formulation stated there is essentially identical to that expressed in Problem 5 of the Notebook. But there is additional confirmation of the authorship . . .
Joseph A. Mussulman
Following Problem 5 in the Notebook are several pages of a “Statistical Table” in Lewis’s hand. In another letter to Jefferson,[3]Autograph letter, signed; recipient’s copy (Library of Congress). Jackson, Letters, 1:56. Patterson writes:
Philada. June 18th 1803.
Sir:
I recommended to Capt. Lewis the use of a Statistical Table in which to set down his astronomical observations, in the course of his intended expedition; as an expedient that would save a great deal of time, and be productive of many other obvious advantages. I had proposed to draw him out a sketch of such a table, but an unusual hurry of business prevented me, while he was in the city. I have now, however, fulfilled my promise and transmit the inclosed for his inspection.
I have sent it under cover to you, Sir, lest Capt. Lewis may have proceeded on his tour; in which case, if you shall judge it worth his notice, you will have the trouble of forwarding it to him. I am Sir with the highest respect & esteem your Obedt. Servt.
R. Patterson
Lewis must have made a copy of the statistical table for his field use on his trip. Following this table there are two pages, also in Lewis’s hand, explaining his procedures for taking and recording astronomical observations together with an entry from Point of Observation No. 21 at the mouth of the Musselshell River (20 May 1805).
In May 1995, Arlen J. Large of Washington, D.C. sent me a copy of the Notebook, having made it from a copy that he had received from Gary Moulton. The pages were 7½ inches tall by 6 5/8 inches wide. As can be expected, the copy (written in the script of the early 1800s), was badly faded in some places, and correspondingly difficult to transcribe.
Determining illegible numbers was a problem only where those numbers could not be derived by performing mathematical operations. Thus, for example, when Patterson gives a series of numbers for “exercises,” it is possible that some misinterpretations were committed.
Abbreviations have been replaced with the spelled-out word unless space in the forms did not permit it. Degree (°), minute (‘) and second (“) marks have been added where they were omitted in the original or expressed only as a ditto sign (“). The words latitude and longitude were almost always capitalized, but not consistently so. They are capitalized here only at the beginning of a sentence.
Only a few additional punctuation marks have been added and those only where ambiguity might otherwise occur. The pages in the manuscript Notebook are unnumbered; page numbers have been inserted in brackets for readers who wish to compare this edition with the original.
Mathematic symbols have been replaced by the word they represent except where there were space limitations in the Forms. They are:
= angle
= moon
= sun
= star
Patterson made a few errors in his numbers and mathematics. They have been identified with footnote symbols in brackets.
Despite Patterson’s assurance to Thomas Jefferson that his astronomical formulas would be “extremely easy even to boys or common sailors of but moderate capacities,” it will soon be obvious that only readers with a working knowledge of trigonometry will find Patterson’s didactic little notebook comprehensible, or even interesting. But then, Lewis evidently had had little or no exposure to higher math prior to his crash courses with the astronomer and surveyor Andrew Ellicott in Lancaster and with Patterson in Philadelphia—in a time span of no more than a few weeks that was crowded with a myriad of other pre-expedition details and obligations. However, anyone should be able to appreciate what a challenge Lewis faced in trying to comprehend these concepts and learning to use them. Indeed, the sheer weight of it should inspire even greater admiration for this young officer for his fortitude in taking on this challenge along with everything else.
Robert N. Bergantino
Butte, Montana
July, 2005
Jefferson’s Request
Washington Mar. 2. 1803[4]Autograph letter signed, sender’s copy; Library of Congess. Jackson, Letters, 1:21. The word “scientific,” in angle-brackets above, was deleted by Jefferson.
Dear Sir
I am now able to inform you, tho’ I must do it confidentially, that we are at length likely to get the Missouri explored, & whatever river heading with that, leads into the Western ocean. Congress by a secret act has authorised me to do it. I propose to send immediately a party of about ten men with Capt. Lewis, my secretary, at their head. If we could have got a person perfectly skilled in botany, natural history, mineralogy, astronomy, with at the same time the necessary firmness of body & mind, habit of living in the woods & familiarity with the Indian character, it would have been better. But I know of no such character who would undertake an enterprise so perilous. To all the latter qualities Capt. Lewis joins a great stock of <scientific> accurate observation on the subjects of the three kingdoms which are found in our own country but not according to their scientific nomenclatures. But he will be able to seize for examination & description such things only as he shall meet with new. He has been for some time qualifying himself for taking observations of longitude & latitude to fix the geographical points of the line he will pass over, but little means are possessed here of doing that; and it is the particular part in which you could give him valuable instruction & he will receive it thankfully & employ it usefully. The instruments thought best to be carried for this purpose are a good theodolite & a Hadley.[5]The theodolite was a device for measuring angles in horizontal and vertical circles simultaneously, which hypothetically would have been quite useful, especially in mapping the Expedition’s … Continue reading He will be in Philadelphia 2. or 3. weeks hence to procure instruments & will take the liberty to call on you; and I shall be particularly obliged to you for any advice or instruction you can give him. I think it adviseable that nothing should be said of this till he shall have got beyond the reach of any obstacles which might be prepared for him by those who would not like the enterprise. Accept assurances of my sincere esteem & great respect.
Th: Jefferson
Patterson’s Reply
Philadelphia March 15 1803[6]Autograph letter signed, recipient’s copy; Library of Congress; Jackson, Letters, 1:28.
Sir
I have been honoured with your favor of the 2d and thank you for your confidence, which I will never abuse. I am preparing a set of astronomical formula for Mr. Lewis and will, with the greatest pleasure, render him every assistance in my power. I take the liberty of subjoining the formula which I commonly use for computing the longitude from the common lunar observation, illustrated by an example. The other formula for computing the time, altitudes, etc., are all expressed in the same manner, viz. by common algebraic signs; which renders the process extremely easy even to boys or common sailors of but moderate capacities
Example
Suppose the apparent angular distance of the sun and moon’s nearest limbs (by taking the mean of a set of observations) to be 110°02’30”, the apparent altitude of
‘s lower limb measuring 20°40’ and that of
‘s lower limb 35°24’, height of the eye 18 feet, estimated Greenwich time September 18th 1798 about 6 hours p.m., time at place of observation, allowing for error of watch, or computed from the sun’s altitude and latitude of place 4h 20m 30s p.m. apparent time. Required the longitude of the place of observation, from the meridian of Greenwich.
Solution
From the apparent altitudes of the lower limbs of
and
find the apparent altitudes of their centers by subtracting the dip corresponding to the height of the eye, and adding the apparent semidiameters: Also from the apparent distance of limbs find the apparent distance of centers by adding the semidiameters. The longitude may then be computed by the following formula, in which the capital letters represent the corresponding arches in the adjoining column; and the small letters, the logarithmic functions of those arches. When the small letter is omitted, the arch is found from the log function. The logs need not be taken out to more than 4 decimal places, and to the nearest minute only of their corresponding arches except in the case of proportional logs. Where an ambiguous sign [. . .] as ± or
(expressing the sum or difference) the one or the other is to be used as directed in the explanatory note to which the number in the margin refers:
110° 02′ 30″ 20° 40′ 00″ 35° 26′ 00″ 15′ 59″ 3′ 18″ 3′ 18″ dip 15′ 20″ 20° 36′ 42″ 35° 20′ 42″ 110° 33′ 49″ apparent distance [of] centers 15′ 59″ 15′ 20″ semidiameter 20° 52′ 41″ 35° 36′ 2″ apparent altitude of centers Explanatory notes
- Add when C is greater than B, otherwise subtract
- Subtract when C is greater than B, otherwise add
- Subtract when either H or I exceeds 90°, or when H is greater than I, otherwise add
- Add when either H or I exceeds 90°, or when H is less than I, otherwise subtract
- In Table 13 (requisite tables) under the nearest degree to Q at the top find two numbers, one opposite the nearest minute to
‘s correction of altitude found in Table 8, and the other opposite the nearest minute to the 1st correction (N) and the difference of those two numbers will be the 3rd correction This correction may generally be omitted.
- Add when Q is less than 90°, Otherwise sub.
- These are to be found in Nautical Almanac from page 8th to page 11th of the month, and the sun or star from which the moon’s distance was observed, taking out the two differences which are the next greater, and next less than the true distance (S) calling that the preceding distance which comes first in the order of time, and the other the following dist.
- The Greenwich time and the time at place of observation must both be reckoned from the same no. [day?]
- When Y is greater than Z the longitude is West, otherwise it is East and when the longitude comes out more than 12 hours or 180° subtract it from 24h or 360° and change its name.

Text version Apparent distance of centers A 110° 33 49 ⋑’s apparent altitude B 35 36 [..csc] b 10.2350 ⊙ or *’s apparent altitude C 20 53 ½ B +C D 28 14 tan d 9.7299 C ∼ D E 7 21 cot e 10.8894 ½A F 55 17 tan f 10.1593 d + e + f – 20 G 80 33 tan — 10.7786 1 F +∼ G H 25 16 2 F + ∼ G I 135 50 tan i 9.9874 ⋑’s horizontal parallax, Nautical Almanac page 7 K 55 42 pr log k .5994 [*] b + i + k – 20 L 27 8 pr log — .8218 [*This should be .5094; 180 ÷ 55’42” = 180÷55.7’=3.231597846; log = 0.5094 see Bowditch, New American Practical Navigator (1802), Tables, p. 137. Because of this error, the remainder of Patterson’s calculation is in error] Refraction of I (considered as an altitude,
Table I (requisite tables)M 59 L – M = 1st correction N 26 9 3 A ± N O 110 7 40 Refraction of H for *, refraction – parallax for ⊙ = 2nd correction P 1 54 4 O ± P Q 110 9 34 5 Correction from Table 13 = 3rd correction R 4 6 Q ± R = true distance of centers S 110 9 30 7 Preceding distance in Nautical Almanac T 110 2 21 7 Following distance in Nautical Almanac U 111 27 47 T ∼ S V 7 9 pr log v 1.4010 T ∼ U W 1 25 26 pr log w 3236 v – w X 15 4 pr log — 1.0774 8 Hour above T in N.A. + X = true Greenwich time Y 6 15 4 8 Time at place of observation Z 4 20 30 9 Y ∼ Z = longitude in time A 1 54 34 9 A ÷ 4 = longitude in degrees, etc. B 28°38½’ West [**] [**Because of the error in Step K, the longitude should be 25°22’30” West] Note, the logarithmetical part of the operation may, with sufficient accuracy be wrought in Gunthers scale thus:
- Extend the compassers from Tangent E to Tangent D, and that extension will reach from Tangent F to Tangent G.
- Extend from Tangent I to sine B and that extent will reach (on the line of numbers) from K to L.
- Extend (on the line of numbers) from W to 180, and that extent will reach from v to X
I am, Sir, with the most perfect respect & esteem, your obedient Servant.
R. Patterson
Transcript
Astronomy Notebook
prepared for
Captain Meriwether Lewis
by
Robert Patterson
Philadelphia, Pennsylvania, 1803[7]Meriwether Lewis Astronomy Notebook, 1803-1805, Western Historical Manuscript Collection—Columbia, Missouri. The Notebook was purchased from a private collector in 1928 by the State Historical … Continue reading
[Page 1:]
Problem 1st
From the altitude of the sun, together with the estimated Greenwich time, and the true hour of the day, apparent time, at place of observation; to compute the latitude of [the] place [of] observation.
Directions
- At any time when the sun is not more than one or two hours from the meridian, but the nearer to the meridian the better, take its altitude and note the time per watch, making allowance for its probable error from true apparent time.
- From the apparent altitude find the true altitude, subtract this from 90° and the remainder will be the zenith distance which call north or south according as the zenith is north or south of the body observed.
[Page 2:]
- Find the true declination of the sun for the estimated Greenwich time.
- From the time at place observation find the hour angle of the sun at the time of observation.
From the above data the latitude may be computed as in the following example.
Note, In all the following Forms, the capital letters signify the corresponding arches in the adjoining column, and the small letters, the sines, tangents, secants &c. of those arches respectively. When the small letter is omitted in the Form, the arch is found from the sine, tangent, &c; but when the small letter is prefixed, the sine, tangent, &c. is found from the arch.
In taking out the sine, tangent, &c. of an arch from the table, or in finding the arch from the sine, tangent &c, it will be sufficient [Page 3:] to take it out to the nearest minute only.
When an ambiguous sign occurs as ± or  the one or the other is to be used as directed in the explanatory note to which the number in the margin refers.
the one or the other is to be used as directed in the explanatory note to which the number in the margin refers.
Example
Suppose the apparent altitude of the sun’s lower limb above the southern horizon = 52°17′, Estimated Greenwich time May 10th 1799 about 17 hours p.m., True apparent time at place of observation = 54m p.m. Required the latitude.

| 52°17′ | “ | 17°41’43” | declination May 10 | |
| 39″ | refraction-parallax | 17°57’12” | ” ” 11 | |
| 52°16’21” | 15’29” | difference | ||
| 15′ 53″ | semidiameter | 10’58” | correction | |
| 52°32’14” | true altitude | 17°52’41” | true declination | |
| 37°27’46” | zenith distance | |||
| 4) 54m | ||||
| 13°30′ | hour angle |
[Page 4:]
Form I.
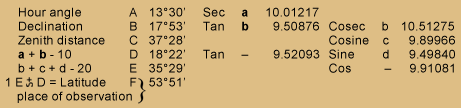
| Hour angle | A | 13°30′ | Sec | a | 10.01217 | ||||
| Declination | B | 17°53′ | Tan | b | 9.50876 | Cosec | b | 10.51275 | |
| Zenith distance | C | 37°28′ | Cosine | c | 9.89966 | ||||
| a + b – 10 | D | 18°22′ | Tan | ‒ | 9.52093 | Sine | d | 9.49840 | |
| b + c + d – 20 | E | 35°29′ | Cos | ‒ | 9.91081 | ||||
1 |
E +∼ D = Latitude place of observation |
}F | 53°51′ |
1 Add when zenith distance and declination are of the same name, otherwise subtract; and the latitude will be of the same name with the greater number.
This rule will give the latitude in all cases where the altitude is taken near the meridian. The rule however may be made universal thus; add when latitude and declination are of the same name, and azimuth of the sun from the meridian less than 90°, also [Page 5:] when the hour angle exceeds 90°; subtract when latitude and declination are of different names, also when azimuth from meridian [is] more than 90°.
Note 1st. When the declination = 0, to the secant of the hour angle add the cosine of the zenith distance, and the sum (abating 10 from the index) will be the cosine of the latitude.
Note 2nd. If an observation be taken both before and after the sun comes to the meridian, when the altitudes are both nearly equal, then a mean of the latitudes computed from these two observations will be more accurate than that computed from one observation; as the errors arising from an error in the watch or time, will in this case tend to correct each other.
[Page 6:]
Examples for Practice
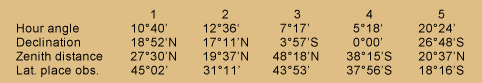
| 1 | 2 | 3 | 4 | 5 | |
| Hour angle | 10°40' |
12°36' |
7°17' |
5°18' |
20°24' |
| Declination | 18°52'N |
17°11'N |
3°57'S |
0°00' |
26°48'S |
| Zenith distance | 27°30'N |
19°37'N |
48°18'N |
38°15'S |
20°37'N |
| Lat. place obs. | 45°02' |
31°11' |
43°53' |
37°56'S |
18°16'S |
Problem 2nd
From two altitudes of the sun together with the intermediate or elapsed time between the two observations and the estimated Greenwich time to compute the latitude of the place.
Directions
- For the proper time when the altitudes are to be taken, consult the remarks in the book of requisite tables pages 21 and 22.
- From the apparent altitudes find the true altitudes.
- Find the declination of the sun for the middle Greenwich time between the two observations.
- [This number and any text possibly associated with it are not in the notebook copy.] [p. 7:]
- Let half the elapsed time be reduced to degrees and minutes.
From the above data the latitude may be computed as in the following example.
Example
Suppose the apparent altitude of the sun’s lower limb at the time of the first observation = 43°28′, time per watch 2h 41m before noon. Apparent altitude at second observation 56°21′, time per watch 30m before noon. Estimated Greenwich time May 12th 1799 about 8 hours p.m. Latitude by account 50°19’N. Required the true latitude?

43°28'00" |
|||
54" |
refraction-parallax |
18°12'23" |
declination May 12 |
43°27'06" |
18°27'16" |
" " 13 |
|
15'52" |
semidiameter |
14'53" |
difference |
43°42'58" |
lesser true altitude |
4'58" |
correction |
56°21' " |
18°17'21" |
true declination North |
|
33" |
71°42'39" |
polar distance |
|
56°20'27" |
2h 41m |
||
15'52" |
30m |
||
56°36'19" |
greater true altitude |
2|2h 11m |
|
4|1h 05m 30s |
|||
∠ of ½ elapsed time |
=16°22½' |
[Page 8:]
Form II

| Polar distance | A | 71°43′ | Tan | a | 10.48097 | Cos | a | 9.49654 | |
| ∠ of ½ elapsed time | B | 16°23′ | Tan | b | 9.46835 | ||||
| 1 | a + b – 10 | C | 84°44′ | Cos | c | 8.96305 | Cot | — | 8.96489 |
| Lesser altitude | D | 43°43′ | |||||||
| Greater altitude | E | 56°36′ | Tan | e | 10.18087 | ||||
| ½ D + E | F | 50°10′ | Tan | f | 10.07875 | ||||
| E ∼ F | G | 6°26′ | Cot | g | 10.94786 | ||||
| a + c – 10 | H | 15°32′ | Tan | h | 9.44402 | ||||
| f + g + h – 20 | I | 18°42′ | Cot | — | 10.47063 | ||||
| H ∼ I | K | 3°10′ | Tan | k | 8.74292 | ||||
| 2 | e + k – 10 | L | 94°48′ | Cos | — | 8.92379 | |||
| 3 | C +∼ L | M | 10°04′ | Sec | m | 10.00674 | Cot | m | 10.75074 |
| e + m – 10 | N | 33° | Cot | n | 10.18761 | Cosec | n | 10.26389 | |
| 4 | A +∼ N | O | 38°43′ | Cot | o | 10.09603 | Sin | o | 9.79621 |
| m + n + o – 20 = | P | 8°47′ | Cos | p | 9.99488 | Cot | — | 10.81084 | |
| H ∠ at Greater alt. o + p – 10 =Latitude at last observation | Q | 50°57′ | Tan | — | 10.09091 | ||||
| 8m 47sec | |||||||||
| /4 | |||||||||
| 35m 8s before noon = time at last observation corrected* | |||||||||
| [*8m 47sec is the Hour Angle of the Greater Altitude shown at P, above. Here Patterson carries the operation one step farther by multiplying the Hour Angle by 4 to obtain the time at last observation, corrected.] | |||||||||
[Page 9:]
- Set down the supplement of the angle found in the table when A is greater than 90°. Let the cosine of C be increased or diminished by as much as a + b—10 exceeds or wants of cotangent C, the nearest arch in the table.
- Set down the supplement of the angle found in the table when I is greater than H.
- Subtract except when A is less than the co-latitude by account and when M exceeds 180° take the cotangent and secant of its excess above 180° and set down the remainder.
- Subtract unless when M is greater than 90°. Note If both altitudes when corrected be equal, the latitude may be found by Problem 1st calling half the elapsed time the true hour of the day or distance (in right ascension) of the body from the meridian. Or if the two altitudes be nearly equal, you may, without any sensible error, take the mean and work as above by Problem 1.
Problem 3d
[Page 10:] From the apparent altitude of the sun, together with the latitude [of the] place [of] observation and estimated Greenwich time; to find the true hour of the day.
Directions
- At any time when the sun is not less than 3 points from the meridian (but the nearer to the East or West points the better) take the altitude.
- From the apparent altitude find the true altitude.
- Find the declination for the estimated Greenwich time, which subtract from 90° when the latitude and declination are of the same name; but add to 90° when they are of different names, and the result will be the polar distance.
From the above data, the hour angle and thence the hour of day may be computed as in the following example.
[Page 11:]
Example
Suppose the apparent altitude of sun’s lower limb west of the meridian 22°35′. Latitude place observation 34°40°N. Estimated Greenwich time May 24, 1799 about 18 hours p.m. Required the time?

| 22°35′ | 20°49’28” | declination May 24 | |
| – 2’06” | parallax-refraction | 21°00’20” | 25 |
| 22°32’54” | 10’52” | difference | |
| + 15’50” | ½ diameter | 8’09” | correction |
| 22°48’44” | true altitude | 20°57’37” | true distance North |
| 69°02’23” | |||
| 34°31’11” | = ½ polar distance |
Form III

| Lat. of place observation | A | 34°40′ | Tan | a | 9.83984 | |
| True altitude | B | 22°49′ | ||||
| ½ A + B | C | 28°44′ | Cot | c | 10.26103 | |
| B ∼ C | D | 5°55′ | Tan | d | 9.01550 | |
| ½ Polar distance | E | 34°31′ | Cot | e | 10.16260 | |
| c + d + e – 20 | F | 15°22′ | Tan | – | 9.43913 | |
| 1. | E +∼ F | G | 19°09′ | Tan | g | 9.54065 |
| 2. | a + g – 10 hour angle | H | 76°06′ | Cos | – | 9.38049 |
| H x 4 = hour in time | I | 5h 05m 24s [5h 04m 24s] | ||||
1. Subtract when A is greater than B, otherwise add.
2. Take the supplement to 180° when F is greater than E.
[Page 12:] Note, When the declination = 0; then to the secant of the latitude add the sine of the altitude, and the sum (abating 10 from the index) will be the cosine of the hour angle.
When the latitude = 0; then to the secant of the declination add the sine of the altitude and the sum (abating 10 from the index) will be the cosine of the hour angle
When the altitude = 0; then to the tangent of the latitude, add the tangent of the declination and the sum (abating 10 from the index) will be the cosine of the hour angle, taking the supplement to 180° when latitude and declination are of the same name.
When both latitude and declination = 0; then the complement of the altitude or zenith distance will be the hour angle.
Problem 4th
Transcript:
[Page 13:] From the latitude of place observation together with the time at place observation and the estimated Greenwich time, to compute the altitude of sun, moon, or any known star.
Directions
- Find the declination of the body for the estimated Greenwich time.
- Find the hour angle of the body at the given time. The altitude may then be computed by Form 4th as in the following examples.
Example 1st
Suppose the latitude 40°N, Greenwich time May 7th 1799 about 17 hours p.m. Time at place observation 3h 42m p.m. Required the true and apparent altitude of sun’s centre.

| 16°53’31” | declination May 7th | |
| 17°09’52” | ” ” 8 | |
| 16’21” | difference | 4| 3h 42m |
| 11’35” | correction | 55°30′ hour angle |
| 17°05’06” | true declination North |
[Page 14:]
Form IV (A)

| Hour angle | A | 55°30′ | Sec | a | 10.24687 | |||||
| Declination | B | 17°06’* | Tan | b | 9.48804 | sin | b | 9.46841 | ||
| a + b – 10 | C | 28°31′ | Tan | — | 9.73491 | cosec | c | 10.32110 | ||
| Latitude | D | 40° | ||||||||
| 1 | C +∼ D | E | 11°29′ | cosec | e | 9.99332** | ||||
| b + c + e – 20 True altitude |
} | F | 37°08′ | sin | — | 9.78073 | ||||
| 2 | Correction of alt. | G | 01′ | |||||||
| 3 | F ± G = apparent altitude |
} | H | 37°09′ |
[* In “Example 1st” Patterson correctly calculates the “true declination North” as 17°05’06”. He errs here in copying it as 17°06′, or 1 mile too far north.]
[** Patterson has written 9.99132 over 9.99332. However, cosecant should read cosine; the log cosine of 11°29′ should be 9.99122, not 9.99132.]
1 Add when latitude and declination are of different names or A greater than 90°; otherwise subtract.
2 For the sun or a star take the refraction corresponding to the altitude Table I. For the moon take the correction Table VIII. These corrections need be taken out only to the nearest minute.
3 Add for the sun or a star; subtract for the moon.
[Page 15:]
Example 2nd
Suppose the latitude 22°40′ N, Greenwich time June 16th 1799 about 15 hours p.m. Time at place observation 11h 32m p.m. Required the true and apparent altitude of the moon’s centre.

| 25°30′ | declination June 16 | 5h 39m 12.4s | right ascension June 16 |
| 26°34′ | ” ” 17 | 5h 43m 21.7s | ” ” ” 17 |
| 1°04′ | difference | 4m 09s | difference |
| 16′ | correction | 2m 36s | correction |
| 25°46′ | ⋑’s declination South | 5h 41m 48s | ⊙’s right ascension |
| 255°17′ | right ascension June 16 | 11h 32m | time at ship |
| 1°58′ | correction | 4| 17h 13m 48s | right ascension mid heaven |
| 257°15′ | ⋑’s right ascension | 258°27′ | ” ” in degrees & minutes |
| 257°15′ | ⋑’s right ascension | ||
| 1°12′ | hour angle |
Form IV (B)
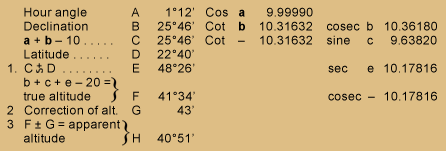
| Hour angle | A | 1°12′ | Cos | a | 9.99990 | |||||
| Declination | B | 25°46′ | Cot | b | 10.31632 | cosec | b | 10.36180 | ||
| a + b – 10 | C | 25°46′ | Cot | — | 10.31632 | sine | c | 9.63820 | ||
| Lat | D | 22°40′ | ||||||||
| 1 | C +∼ D | E | 48°26′ | sec. | e | 10.17816 | ||||
| b +c +e – 20= true altitude |
} | F | 41°34′ | cosec. | — | 10.17816 | ||||
| 2 | Correction of alt. | G | 43′ | |||||||
| 3 | F ± G = apparent altitude |
} | H | 40°51′ |
Example 3d
Suppose the latitude 45°10′ N, Greenwich time January 31, 1799 about 18 hours p.m. Time at place observation 12h 40m p.m. Required the true and apparent altitude of the star Aldebaran?

| 16°03’02” | [declination] | 20h 56m 44s | [⊙’s right ascension 31 Jan] |
| 2’37” | correction | 21h 00m 49s | [⊙ right ascension 1 Feb] |
| 16°05’37” | *’s declination North | 4m 05s | [difference] |
| 3m 04s | [correction] | ||
| 4h 23m 19s | [*’s right ascension] | 20h 59m 48s | sun’s right ascension |
| 1m 05s | correction | 12h 40m | time at ship |
| 4h 24m 24s | *’ s right ascension | 33h 39m 48s | |
| 24h | |||
| By Form 4th (A) | 9h 39m 48s | right ascension mid-heaven | |
| 4h 24m 24s | |||
| 4|5h 15m 24s | |||
| 78°51′ * hour angle |
| A | 78°51′ | 10.71359 | |
| B | 16°06′ | 9.46035 | 9.44297 |
| C | 56°11′ | 10.17394 | 10.08049 |
| D | 45°10′ | ||
| E | 11°01′ | 9.99192 | |
| F | 19°07′ | 9.51538 | |
| G | 03′ | ||
| H | 19°10′ |
[Page 17:] Note When the declination = 0; then to the cosine of the latitude add the cosine of the hour angle and the sum (abating 10 from the index) will be the sine of the true altitude.—
And when the latitude = 0; then to the cosine of the declination add the cosine of the hour angle and the sum (abating 10 from the index) will be the sine of the true altitude.
When both latitude and declination = 0; then the complement of the hour angle will be the true altitude.
Examples for practice
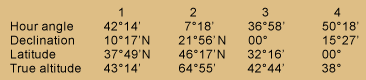
| 1 | 2 | 3 | 4 | |
| Hour angle | 42°14′ | 7°18′ | 36°58′ | 50°18′ |
| Declination | 10°17’N | 21°56′ | 00° | 15°27′ |
| Latitude | 37°49’N | 46°17′ | 32°16′ | 00° |
| True altitude | 43°14′ | 64°55′ | 42°44′ | 38° |
[Page 18:]
Problem 5th
To find the Longitude by Lunar observation
Directions
- At any time when the sun and moon, or the moon and any of the stars from which her distance is calculated in the Nautical Almanac[8]A Nautical Almanac is a yearbook for navigators and astronomers, containing the predicted positions of the sun, moon, and planets with respect to Earth, every day of the year. The first one was … Continue reading on the given day, are both visible, and neither of the bodies less than 5° high; your instrument being previously adjusted, or the index error ascertained, and also the error of your watch found by a previous observation as directed [in] problem 3d, take a set of three or more observations of the apparent angular distance of the sun and moon’s nearest limbs, or of the star from the moon’s nearest or farthest limb, viz. that which is fully enlightened, noting the corresponding times per watch; and at the time that you measure the distance, let two [Page 19:] assistants take the altitudes of the bodies, respectively. Or the distances and the altitudes may all be taken by the same observer, at small equal intervals of time in the following order, viz.,
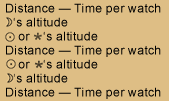 Distance — Time per watch
Distance — Time per watch
Moon’s altitude
Sun or Star’s altitude
Distance — Time per watch
Sun or Star’s altitude
Moon’s altitude
Distance — Time per watch - Of these distances, times and altitudes, take means by dividing their respective sums by the number of observations.
- Let the mean altitudes be so far corrected as respects semidiameter, so as to obtain the apparent altitudes of the centres above the true horizon.
- To the apparent distance of sun and moon’s nearest limbs add the sun’s semidiameter, Nautical Almanac page III, [Page 20:] of the month, and also the moon’s semidiameter, Nautical Almanac page VII of the month, increased by the augmentation, Table IV. When the distance of a star from the moon’s nearest limb is observed, you must add the moon’s semidiameter + augmentation; but when the star’s distance from the moon[‘s] farthest limb is observed, you must subtract the semidiameter + augmentation; and thus you will have the apparent distance of the centres of the bodies observed.
- If at the time of taking the above observations, one of the bodies (but especially the sun) be not less than 3 or 4 points of the compass [33¾°- 45°] from the meridian, the time at place observation may be computed from the altitude of the body, as in Problem III independently of the time per watch, and this should always be done when circumstances admit.
- As it may frequently happen that the altitudes [Page 21:] of one or both of the bodies cannot well be taken you must then compute the apparent altitudes by problem 4th, and this method is generally to be preferred on land.
From the above data, the longitude of place observation may be computed as in the following example.
Example
Suppose the apparent angular distance of the sun and the moon’s nearest limbs (by taking the mean of a set of observations) to be 83°30’04”. The apparent altitude of the sun’s lower limb measuring 52°44′ and that of the moon’s lower limb 24°32′, Greenwich time September 22, 1799 about 9 hours p.m. Time at place observation (allowing for error of watch from true apparent solar time) 15 hours p.m.
Required the longitude of place observation from the meridian of Greenwich?
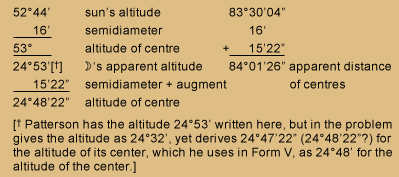
52°44' |
sun's altitude |
83°30'04" |
|
16' |
semidiameter |
16' |
|
53° |
altitude of centre |
+ 15'22" |
|
24°53' * |
⋑'s apparent altitude |
84°01'26" |
apparent distance of centres |
15'22" |
semidiameter+augment |
||
24°47'22" |
altitude of centre |
[* Patterson has the altitude 24°53′ written here, but in the problem, gives the altitude as 24°32′, yet derives 24°47’22” (24°48’22”?) for the altitude of its center, which he uses in Form V, as 24°48′ for the altitude of the center.]
[Page 22:]
Form V
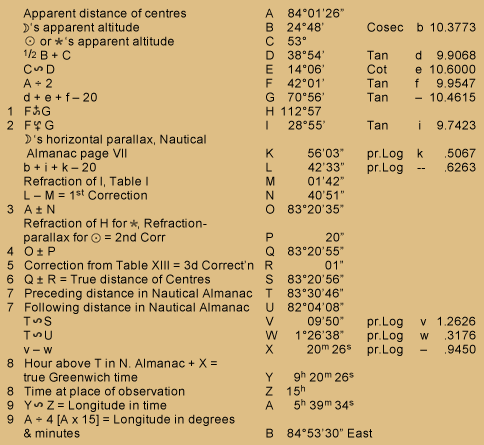
| apparent distance of centres | A | 84°01'26" |
||||
| ⋑’s apparent altitude | B | 24°48' |
Cosec | b | 10.3773 | |
| ⊙ or *’s apparent altitude. | C | 53° |
||||
| ½ B + C . | D | 38°54' |
Tan | d | 9.9068 | |
| C ∼ D | E | 14°06' |
Cot | e | 10.6000 | |
| A ÷ 2 | F | 42°01' |
Tan | f | 9.9547 | |
| d + e + f – 20 | G | 70°56' |
Tan | – | 10.4613 | |
| 1 | F +∼ G | H | 112°57' |
|||
| 2 | F ∼+ G | I | 28°55' |
Tan | i | 9.7423 |
| ⋑’s horizontal parallax, Nautical Almanac page VII . | K | 56'03" |
pr.Log | k | .5067 | |
| b + i + k – 20 | L | 42'33" |
pr Log | – | .6263 | |
| Refraction of I, Table I | M | 01'42" |
||||
| L – M = 1st Correction | N | 40°51" |
||||
| 3 | A ± N | O | 83°20'35" |
|||
| Refraction of H for*, Refraction-parallax for ⊙ = 2nd Corr | P | 20" |
||||
| 4 | O ± P | Q | 83°20'55" |
|||
| 5 | Correction from Table XIII = 3d Correction | R | 01" |
|||
| 6 | Q ± R = True distance of Centres | S | 83°20'56" |
|||
| 7 | Preceding distance in Nautical Almanac | T | 83°30'46" |
|||
| 7 | Following distance in Nautical Almanac | U | 82°04'08" |
|||
| T ∼ S | V | 9'50" |
pr Log | v | 1.2626 | |
| T ∼ U | W | 1°26'38" |
pr Log | w | .3176 | |
| v – w | X | 20m 26s |
pr Log | – | .9450 | |
| 8 | Hour above T in N. Almanac+X = true Greenwich time | Y | 9h 20m 26s |
|||
| 8 | Time at place of observation | Z | 15h |
|||
| 9 | Y ∼ Z = Longitude in time | A | 5h 39m 34s |
|||
| 9 | A ÷ 4 [A x 15]= Longitude in degrees & minutes | B | 84°53'30" |
East |
[Page 23:]
- Add when C is greater than B, otherwise subtract.
- Subtract when C is greater than B; otherwise add.
- Subtract when either H or I exceeds 90°; or when H is greater than I.
- Add when either H or I exceeds 90°; or when H is less than I.
- In Table VIII find the correction of moon’s altitude, then in Table XIII under the nearest degree to Q at the top, find two numbers; one opposite to the nearest minute to moon’s correction of altitude found as above, and the other opposite the nearest minute to first correction (N) and the difference of these two numbers will be the third correction. This correction may, without sensible [error], be generally omitted.
- Add when Q is less than 90°, otherwise subtract.
- These are to be found in Nautical Almanac from page 8th to page 11th of the month opposite the day of the month and the sun or the star from which the moon’s distance was observed; taking out the two distances, which are next greater and next less than the true distance (S) calling that the preceding distance which comes first in the order of time and the other the following distance.[Page 24:]
- The Greenwich time and time at place observation must both be reckoned from the noon of the same day.
- When the true Greenwich time is greater than the time at place observation the longitude is west; otherwise it is east. When a longitude comes out more than 12 hours or 180°, subtract it from 24 hours or 360° and change its name. ––
Example 2nd
Suppose the apparent angular distance of the star Regulus from the moon’s farthest limb to measure 54°18′, apparent altitude of moon’s lower limb 20°10′, apparent altitude of star 58° 32′, Greenwich time November 23d about 17 hours p.m. Time at place observation allowing for error of watch 17h 20m 25sec p.m. Required the longitude?

20°10' |
|
16'38" |
semidiameter + augmentation |
20°26'38" |
moon’s apparent altitude |
54°18' |
[apparent angular separation] |
16'38" |
|
54°01'22" |
apparent distance |
[Page 25:]
This table, not in the notebook, is provided by the editor by way of explanation:

| [apparent distance] | A | 54°01'22" |
|
| [moon’s apparent altitude] | B | 20°27' |
10.4567 |
| [star’s apparent altitude] | C | 58°32' |
|
| [½ (B+C)] | D | 39°29' |
9.9159 |
| [C + ∼ D] | E | 19°03' |
10.4618 |
| [A ÷ 2] | F | 27°01' |
9.7075 |
| [d+e+f-20] | G | 50°35' |
10.0852 |
| [F+∼ G] | H | 77°36' |
|
| [F+∼ G] | I | 23°34' |
9.6397 |
| [moon’s horizontal parallax] | K | 60'42" |
0.4721 |
| [b+i+k–20] | L | 48'37" |
0.5685 |
| [refraction of I] | M | 02' 7" |
|
| [L-M, 1st correction] | N | 46'30" |
|
| [A ± N] | O | 53°14'52" |
|
| [refraction of H] | P | 12" |
|
| [O ± P] | Q | 53°14'40" |
|
| [corr Table XIII, 3rd corr] | R | 06" |
|
| [Q ± R, true distance] | S | 53°14'46" |
|
| [preceding distance NA] | T | 52°17'44" |
|
| [following distance NA] | U | 54°08'17" |
|
| [T∼ S] | V | 57'02" |
0.4991 |
| [T∼ U] | W | 1°50'33" |
0.2117 |
| [v – w] | X | 1h 32m 52s |
0.2874 |
| [hour above T] | Y | 16h 32m 52s |
|
| [time at place observation] | Z | 17h 20m 25s |
|
| [Y – Z, longitude in hours] | A | 47m 33s |
|
| [A x 15] | B | 11°53¼ East |
[Thus ends the five-part instruction manual in celestial observation that mathematician-astronomer Robert Patterson prepared especially for Meriwether Lewis. Below, perhaps at Patterson’s suggestion, Lewis laid out a table in which data from his own observations could be entered in an orderly manner. However, he never used it, nor did he ever follow any similar plan for recording his field observations; had he done so, it might have been easier for another person to calculate, or recalculate, the desired latitudes, longitudes, declinations, chronometer errors, and so on.]
[Lewis’s notes]
Patterson’s Statistical Table
Immediately following Patterson’s document appear, in Lewis’s handwriting, these Statistical Tables, undoubtedly those recommended by Patterson in his letter to Jefferson of June 18, 1803. The columns extend across four double pages (13¼ in. x 7½ in.). There are no entries but the headings in any of the columns.
Patterson’s Statistical Table Written in Lewis’s Hand
Courtesy State Historical Society of Missouri, digital.shsmo.org/cdm/ref/collection/frontier/id/169. Images are in the Public Domain.
Transcription
[Pages 26–27]
Statistical Table.
- 1. Place of observation
- 2. Date of obs. Astronomical
- 3. Hour of the Day apt. Time at place obs Astroncl. P.M.
- 4. Hour of the day mean Time P.M. astronl.
- 5. Hour of the day pr. watch. P.M. astrl.
- 6. Error of the watch on mean time f. s.
- 7. Daily gain or loss of watch on mean time. g. s.
- 8. Apt. altd. of ⊙’s center, lower or upper limb ⊙. LL. UL.
- 9. true altd. of ⊙’s center.—
- 10. Apt. altd. of ⋑’s center Lower or upper li-mb ⊖. LL. UL.
- 11. true altd. ⋑’s center.—
- 12. Error of the instrument employed in obstn. B. F.
- 13. Star’s name
[Pages 28–29]
Statistical Table. Continued
- rept. 2. Date of Obs. Astronomical
- 14. Apparent altd. of Star
- 15. app. distance ⊙’s & ⋑’s Nearest limbs. ⊙ E. or W.
- 16. app. dist. of ⋑ & * The * E. or W.
- 17. true distance of Centers.
- 18. Longitude of place from Greenwich
- 19. Latitude of place
- 20. Magnetic azamuth of ⊙ or pole *.
- 21. True azimuth of ⊙ or pole *.—
- 22. Variation of Magnetic needle.—
- Miscellanious remarks.—
May 21st 1805 Point of observation No. 22.
On the Lard. shore at the commencement of the 5th course of this day observed time and distance of the ![]() ‘s and moon’s nearest limbs, the
‘s and moon’s nearest limbs, the ![]() East— with Sextant
East— with Sextant

| Mean of a Set of 12 Observations | |
|---|---|
| Time | Distance |
| A.M. 9h 25m 35s | 91° 45′ 19" |
Explanation and notes
on the foregoing table
c. denotes – that the numbers to which it is prefixed is the result of calculations . —
ob. Denotes that the numbers to which it is prefixed are the result of observation only and remain to be calculated.
f. or s. in collumn 5th denotes that the watch is too fast or slow the number of minutes seconds &c to which it is prefixed. —
g. or l. denotes gain or loss of watch.
⊙. LL. or U.L. Denote sun’s center, his Lower Limb, or Upper Limb. —
B or F denote the back or Fore observation – it may be well here to remark that all the back observations are made with an octant & artificial horizon, and that the apparent altitudes as set down in collumns No. 8, 10 & 14 where the instrument error is designated B. are always to be understood to express the number of Degrees ‘ & ” be shewn by the graduated limb of the octant at the time of the observation, and is the complyment only of 180° or the double altitude of the object observed. Thus the sum given by the back observation as set down in the table are subtracted from 180° and the remainder is the double apparent altitude of the object observed, which divided by 2 and is the same.
[Page 31, in Lewis’s hand:]
![]() the post meridian observation of the preceding [i.e., following] observation was made at the entrance of the Musselshell River.————
the post meridian observation of the preceding [i.e., following] observation was made at the entrance of the Musselshell River.————
Point of observation No. 21.
May 20th 1805
At the point of land formed by the junction of the Musselshell River and the Missouri. observed meridian altitude of ![]() ‘s L.L. with octant by the back observation —————————————— 59°50′ -“
‘s L.L. with octant by the back observation —————————————— 59°50′ -“
Latitude deduced from this observation 47. 00. 24.6

| Observed Magnetic azimuth of ⊙’s Center.— | |||
|---|---|---|---|
| Azimuth by Circumferentor |
Time by Chronometer |
Altitude by Sextant of ⊙’s LL. |
|
| 1st | S 85° W. |
6h 14m 35s |
50° ' " |
|
|
|
|
| 2nd | S 82 W. |
" 24 36 |
46 37 30 |
| 3rd | S 80 W. |
" 34 42 |
43 15 30 |
[transcript end]
May 21st 1805 Point of observation No. 22.
On the Lard. shore at the commencement of the 5th course of this day observed time and distance of the ![]() ‘s and moon’s nearest limbs, the
‘s and moon’s nearest limbs, the ![]() East— with Sextant
East— with Sextant

| Mean of a Set of 12 Observations | |
|---|---|
| Time | Distance |
| A.M. 9h 25m 35s | 91° 45′ 19" |
Not only did Lewis never employ the Statistical Tables sketched out above, he never consistently used all of the abbreviations listed in the “Explanation and notes.” Curiously, the material that follows on the very next page indicates that he carried the Astronomy Notebook throughout the expedition, for there he entered data relating to the Meridian Altitude he and Clark observed at the confluence of the Missouri and Musselshell Rivers on 20 May 1805.
The first data set is similar to the one in Clark’s journal entry (Moulton, 4:174), except that Clark’s second bearing reads S85°W there, whereas Lewis recorded S83°W, which would have been closer to correct. Lewis, unfortunately, arrived at 58 degrees for the sun’s altitude, which obviously is wrong. Clark, either while he and Lewis were taking the observation or else from the notes of whoever was helping Lewis at the time, wrote down a double altitude of the sun’s lower limb as 48°20’15”, which was about right. Maybe Lewis was using this page as a worksheet for a discussion with Clark, and simply crossed out the whole second line containing his erroneous conclusion, without seeing any need to revise it.
The Lunar Distance Lewis deduced from an unrecorded set of 12 observations on the 21st, at Point of Observation No. 22, is identical to the entry in his journal (Moulton, 4:177) as far as the figures are concerned.
Notes
| ↑1 | Autograph document signed; sender’s copy (Library of Congress). Reprinted in Donald Jackson, ed., Letters of the Lewis and Clark Expedition with Related Documents, 1783-1854, 2d ed., 2 vols. (Urbana: University of Illinois Press, 1978), 1:61-62. |
|---|---|
| ↑2 | Ibid., 1:28-31. |
| ↑3 | Autograph letter, signed; recipient’s copy (Library of Congress). Jackson, Letters, 1:56. |
| ↑4 | Autograph letter signed, sender’s copy; Library of Congess. Jackson, Letters, 1:21. The word “scientific,” in angle-brackets above, was deleted by Jefferson. |
| ↑5 | The theodolite was a device for measuring angles in horizontal and vertical circles simultaneously, which hypothetically would have been quite useful, especially in mapping the Expedition’s route. However, as Lewis explained in a letter he wrote to Jefferson on May 14, 1803, “Mr. Patterson and Mr. Ellicott both disapprove of the Theodolite as applicable to my purposes; they think it a delicate instrument, difficult of transportation, and one that would be very liable to get out of order; they also state that in it’s application to any observations for obtaining the Longitude, it would be liable to many objections, and to much more inacuracy than the Sextant.” Jackson, Letters, 1:48. “Hadley” refers to Hadley’s quadrant, properly called an octant. In Philadelphia Lewis purchased “1 Hadleys Quadrant with Tangt Screw,” which he later (July 22, 1804; Moulton, Journals, 2:411) described as “A common Octant of 14 Inches radius, graduated to 20′, which by means of the nonius was devisibile to 1′, half of this sum, or 30” was perceptible by means of a micrometer. this instrument was prepared for both the fore and back observation; her error in the fore observation is 2°+, & in the back observtion 2°11’40.3″+ “[A]t the time of our departure from the River Dubois untill the present moment [near the mouth of the Platte River], the sun’s altitude at noon has been too great to be reached with my sextant, for this purpose I have therefore employed the Octant by the back observation. the degrees ‘ & “, recorded for the sun’s altitude by the back observation express only the angle given by the graduated limb of the instrument at the time of observation, and are the complyment of the double Altitude of the sun’s observed limb; if therefore the angle recorded be taken from 180° the remainder will be the double altitude of the observed object, or that which would be given by the fore observation with a reflecting surface.” |
| ↑6 | Autograph letter signed, recipient’s copy; Library of Congress; Jackson, Letters, 1:28. |
| ↑7 | Meriwether Lewis Astronomy Notebook, 1803-1805, Western Historical Manuscript Collection—Columbia, Missouri. The Notebook was purchased from a private collector in 1928 by the State Historical Society of Missouri as part of the Breckenridge Collection. This is the first appearance of the entire document in print. |
| ↑8 | A Nautical Almanac is a yearbook for navigators and astronomers, containing the predicted positions of the sun, moon, and planets with respect to Earth, every day of the year. The first one was published in London in 1766. Three items listed as “Nautical Ephemeris” appear in the summary of purchases Lewis made in preparation for the expedition. |






