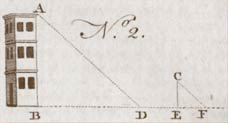Tools and Techniques / Measuring Heights and Distances

Measuring Heights and Distances

From Owen's Dictionary

By Joseph A. Mussulman

Text and images from “Heights and Distances,” A Dictionary of Arts and Sciences (1754), in the small reference library carried by Lewis & Clark:

The measuring of heights or distances is of two kinds: when the place or object is accessible, as when you can approach to its bottom; or inaccessible, when it cannot be approached.

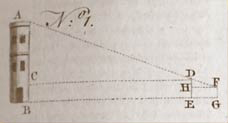
Prob. I. To measure an accessible height AB, by means of staffs. Fig. 1, No 1.

Figure 1

No. 1

A medieval tower with lines drawn from a single point to its base and top

“Let there be placed perpendicularly to the ground, a longer staff DE, like wise a shorter one, FG, so as to the observatory may see A, the top of the height to be measured, over the side D, F, of the two staffs; let FH and DC, parallel to the horizon, meet DE and AB in H and C: then the angles FHD, DCA, shall be equi-regular; for the angles at C and B right ones: likewise the angle A is equal to FDH; wherefore the remaining angles are also equal. Therefore as FH, the distance of the two staffs, is to HD, the excess of the longer staff above the shorter, so is DC, the distance of the longer staff from the tower, to CA, the of the height of the tower above the longer staff: and thence CA will be found by the rule of three.[1]“It is called the Rule of Three from having three numbers given to find a fourth but more properly, the Rule of Proportion, because by it we find a fourth number proportional to three given … Continue reading To which if the length DE be added, you will have the whole height of the tower BA.”

 

Another method may be occasionally contrived for measuring an inaccessible height, as by the given length of the shadow BD (No 2.).

Figure 2

No. 2

a medieval tower being measured using two separate triangles

To find the height AB: let there be a staff CE, perpendicularly, producing the shadow EF: then it will be as EF, the shadow of the staff, is to EC, the staff itself; so is BD, the shadow of the tower, to BA, the height. Though the plane on which the shadow of the tower falls, be not parallel to the horizon, if the staff be erected in the same plane, the rule will be the same.

 

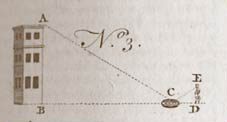
Prob. II. To measure an accessible height by means of a plain mirrour.

Figure 3

No. 3

a medieval tower with a line going from its base to a mirror on the ground, then reflected to its top

Let AB (No 3.) be the height to be measured; let the mirrour be placed at C, in the horizontal plane BD, at a known distance BC: let the observer go back to D, till he see the image of the summit in the mirrour, at a certain point of it, which he must diligently mark, and let DE be the height of the observer’s eye. The triangles ABC and EDC, are equiangular; for the angles at D and B are right angles; and ACE, ECD, are equal, being the angles of incidence and reflection of the ray AC; wherefore the remaining angles at A and E, are also equal. Therefore it will be as CD is to DE; so is CD to BA.”

“Note 1. The observer will be more [able?] if, at the point D, a staff be placed in the ground perpendicularly, over the top of which the observer may see a point of the glass exactly in a line betwixt him and the tower.”

“Note 2. In place of a mirrour may be used the surface of water, which naturally becomes parallel to the horizon.”

 

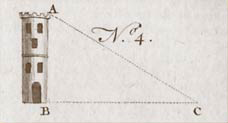
Prob. III. To measure an accessible height by the geometrical quadrant, theodolite,[2]Jefferson had recommended to Lewis that he take a theodolite, with which both horizontal and vertical angles could be measured. However, Andrew Ellicott and Robert Patterson, Lewis’s mentors on … Continue reading &c.

Figure 4

No. 4

A triangle with a mideival tower as one side, the ground as the other, and the hypotenuse in the air

Let the angle C (ibid. No 4.) be found. Then in the triangle ABC, right-angled at B (BC being supposed the horizontal distance of the observer from the tower) having the angle C, and the side BC, the required height will be found by the first case of plain trigonometry. Thus, suppose the angle C, 37° 24′, and the horizontal distance, BC 226, then the proportion will be as R:T.[L] C::CB:BA, the height.

 

Prob. IV. To measure an inaccessible height by the geometrical quadrant, &c. at two stations.

Figure 5

No. 5

A medieval spire with two triangles drawn from its top to two points in the ocean

Let the angle ACB be observed (ibid. no 5.) , then let the observer go from C, to the second station D, in the rightline BCD; and after measuring this distance CD, take the angle ADC likewise with the quadrant. Then in the triangle ACD, which is formed by the two visual rays AD, AC, and the distance of the two stations D and C, there is given the angle ADC, with the angle ACD, because the angle ACB was given before; therefore the remaining angle CAD is given likewise. But the distance of the stations C and D is also given; therefore by the second case of oblique-angled trigonometry,[3]Owen’s Dictionary, s.v. Trigonometry: “Case II. The angles and one of the legs given, to find the hypothenuse. Example: In the triangle ABC, (ibid. no 4.) suppose AB 124, and the angle A … Continue reading the side AC will be found. Wherefore, in the right-angled triangle ABC, all the angles and hypothenuse AC are given; consequently by the third case of plain trigonometry,[4]Ibid.: “Case III. The angles and hypothenuse given, to find either of the legs. Example: In the triangle ABC, &suppose the hypothenuse AC = 146, and the angle A = 36°14 .; consequently the … Continue reading the height sought, AB, may be found; as also the distance of the station C, from AB, the perpendicular within the hill or inaccessible height.

 

Figure 6

No. 6

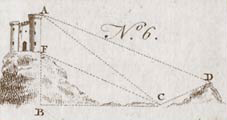
A medieval tower on a high hill with one triangle drawn from the ground and another from the top of a smaller hill

If the height of the tower is wanted, the angle BCF (ibid. no 6.) may be found with the quadrant, which being taken from the angle ACB already known, the angle ACF will remain; but the angle FAC was known before; therefore the remaining angle AFC will be known. But the side AC was supposed found by the last problem; therefore in the triangle AFC, all the angles, and one of the sides AC being known, AF the height of the tower above the hill may be found by trigonometry.

 

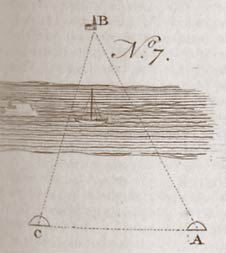
Prob. V. To measure the distance of two places A and B, of which one, A is accessible, by the theodolite, &c. ibid. no 7.

Figure 7

No. 7

A triangle with a vertice across a river connecting two different points on the near shore

Let there be erected at two points, A and C (sufficiently distant) visible signs; then let the two angles BAC, BCA, be taken by the theodolite. Let the distance of the stations A and C be measured with a chain. Then the third angle being known, and the side AC; therefore, by the second case of oblique trigonometry, the distance required AB, will be found.

[This is the method Clark probably used to measure the widths of rivers. If he were not at ease with the “second case of oblique trigonometry,” he could have plotted the angles and distances on graph paper using his circular protractor with the index arm.]

 

Editor note: We’ll probably never know with any certainty how to interpret Clark’s phrase, “Spirit leavels &c.,” and it really doesn’t matter. All that matters is that he “took the hight with as much accuracy as possible.” We may interpret that literally.

Notes

Notes
↑1 “It is called the Rule of Three from having three numbers given to find a fourth but more properly, the Rule of Proportion, because by it we find a fourth number proportional to three given numbers: and because of the necessary and extensive use of it, it is called the Golden Rule.” s.v. Proportion: “When two quantities &are compared, the former term is called the antecedent and the latter the consequent. . . . Thus the ratio of . . . two numbers in geometrical proportion, is found by dividing the antecedent by the consequent, and the quotient is the exponent or denominator of the ratio.” Owen’s Dictionary, Rule of Three.
↑2 Jefferson had recommended to Lewis that he take a theodolite, with which both horizontal and vertical angles could be measured. However, Andrew Ellicott and Robert Patterson, Lewis’s mentors on such matters, advised against it on the grounds that the instrument was too fragile to be dependable. Instead, Lewis took an octant. Donald Jackson, Letters of the Lewis and Clark Expedition, with Related Documents, 1783-1854 (2nd ed., 2 vols., Champaign: University of Illinois Press, 1975), 1:48.
↑3 Owen’s Dictionary, s.v. Trigonometry: “Case II. The angles and one of the legs given, to find the hypothenuse. Example: In the triangle ABC, (ibid. no 4.) suppose AB 124, and the angle A 34°, 20 .; consequently the angle C 55°, 40 . required the hypothenuse AC, in the same parts with AB. &Geometrically, & the hypothenuse, AC, is found, by taking its length in your compasses, and applying that to the same line of equal parts from which AB was taken.”
↑4 Ibid.: “Case III. The angles and hypothenuse given, to find either of the legs. Example: In the triangle ABC, &suppose the hypothenuse AC = 146, and the angle A = 36°14 .; consequently the angle C = 53° 35 .; required the leg AB. &Geometrically: draw the line AB at pleasure, and make the angle BAC equal to 36°, 25 .; then take AC equal to 146 from any line equal parts; lastly, from the point C, let fall the perpendicular CB, on the line AB. So the triangle is constructed, and AB may be measured from the line of equal parts.”

Discover More

  • The Lewis and Clark Expedition: Day by Day by Gary E. Moulton (University of Nebraska Press, 2018). The story in prose, 14 May 1804–23 September 1806.
  • The Lewis and Clark Journals: An American Epic of Discovery (abridged) by Gary E. Moulton (University of Nebraska Press, 2003). Selected journal excerpts, 14 May 1804–23 September 1806.
  • The Lewis and Clark Journals. by Gary E. Moulton (University of Nebraska Press, 1983–2001). The complete story in 13 volumes.

This page was funded in part by a grant from the Montana Cultural Trust.

This site is provided as a public service by the
Logo: Lewis & Clark Trail Heritage Foundation
Lewis and Clark Trail Heritage Foundation
with cooperation and funding from the following organizations:

Unless otherwise noted, journal excerpts are from The Journals of the Lewis and Clark Expedition, edited by Gary E. Moulton, 13 vols. (Lincoln: University of Nebraska Press, 1983-2001).